4.10 Searching for minima and maxima of functions
The minimize and maximize commands can be used to find the minima or maxima of algebraic expressions. In each case, a single algebraic expression should be supplied for optimisation, together with a comma-separated list of the variables with respect to which it should be optimised. In the following example, a minimum of the sinusoidal function 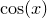 is sought:
is sought:
pyxplot> set numerics real
pyxplot> x=0.1
pyxplot> minimize cos(x) via x
pyxplot> print x/pi
1
Note that this particular example doesn’t work when complex arithmetic is enabled, since 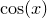 diverges to
diverges to 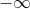 at
at 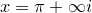 .
.
Various caveats apply both to the minimize and maximize commands, as well as to the solve command. All of these commands operate by searching numerically for optimal sets of input parameters to meet the criteria set by the user. As with all numerical algorithms, there is no guarantee that the locally optimum solutions returned are the globally optimum solutions. It is always advisable to double-check that the answers returned agree with common sense.
These commands can often find solutions to equations when these solutions are either very large or very small, but they usually work best when the solution they are looking for is roughly of order unity. Pyxplot does have mechanisms which attempt to correct cases where the supplied initial guess turns out to be many orders of magnitude different from the true solution, but it cannot be guaranteed not to wildly overshoot and produce unexpected results in such cases. To reiterate, it is always advisable to double-check that the answers returned agree with common sense.
Example: Finding the maximum of a blackbody curve
When a surface is heated to any given temperature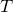 , it radiates thermally. The amount of electromagnetic radiation emitted at any particular frequency, per unit area of surface, per unit frequency of light, is given by the Planck Law:
, it radiates thermally. The amount of electromagnetic radiation emitted at any particular frequency, per unit area of surface, per unit frequency of light, is given by the Planck Law:
The visible surface of the Sun has a temperature of approximately 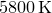 and radiates in such a fashion. In this example, we use the solve, minimize and maximize commands to locate the frequency of light at which it emits the most energy per unit frequency interval. This task is simplified as Pyxplot has a system-defined mathematical function Bv(nu,T) which evaluates the expression given above.
and radiates in such a fashion. In this example, we use the solve, minimize and maximize commands to locate the frequency of light at which it emits the most energy per unit frequency interval. This task is simplified as Pyxplot has a system-defined mathematical function Bv(nu,T) which evaluates the expression given above.
Below, a plot is shown of the Planck Law for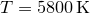 to aid in visualising the solution to this problem:
to aid in visualising the solution to this problem:
![\includegraphics[width=\textwidth ]{examples/eps/ex_eqnsolve}](images/img-0148.png)
To search for the maximum of this function using the maximize command, we must provide an initial guess to indicate that the answer sought should have units of Hz:
pyxplot> nu = 1e14*unit(Hz)
pyxplot> maximize phy.Bv(nu,5800*unit(K)) via nu
pyxplot> print nu
340.9781 THz
This maximum could also be sought be searching for turning points in the function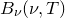 , i.e. by solving the equation
, i.e. by solving the equation
This can be done as follows:
pyxplot> nu = 2e14*unit(Hz)
pyxplot> solve diff_dv(phy.Bv(v,5800*unit(K)),nu) =
.......> unit(0*W/Hz**2/m**2/sterad) via nu
pyxplot> print nu
340.9781 THz
Finally, this maximum could also be found using Pyxplot’s built-in function Bvmax(T):
pyxplot> print phy.Bvmax(5800*unit(K))
340.97806 THz
When a surface is heated to any given temperature
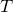 , it radiates thermally. The amount of electromagnetic radiation emitted at any particular frequency, per unit area of surface, per unit frequency of light, is given by the Planck Law:
, it radiates thermally. The amount of electromagnetic radiation emitted at any particular frequency, per unit area of surface, per unit frequency of light, is given by the Planck Law: ![\[ B_\nu (\nu ,T)=\left(\frac{2h^3}{c^2}\right)\frac{\nu ^3}{\exp (h\nu /kT)-1} \]](images/img-0144.png) |
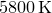 and radiates in such a fashion. In this example, we use the solve, minimize and maximize commands to locate the frequency of light at which it emits the most energy per unit frequency interval. This task is simplified as Pyxplot has a system-defined mathematical function Bv(nu,T) which evaluates the expression given above.
and radiates in such a fashion. In this example, we use the solve, minimize and maximize commands to locate the frequency of light at which it emits the most energy per unit frequency interval. This task is simplified as Pyxplot has a system-defined mathematical function Bv(nu,T) which evaluates the expression given above. Below, a plot is shown of the Planck Law for
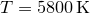 to aid in visualising the solution to this problem:
to aid in visualising the solution to this problem: ![\includegraphics[width=\textwidth ]{examples/eps/ex_eqnsolve}](images/img-0148.png)
To search for the maximum of this function using the maximize command, we must provide an initial guess to indicate that the answer sought should have units of Hz:
pyxplot> nu = 1e14*unit(Hz)
pyxplot> maximize phy.Bv(nu,5800*unit(K)) via nu
pyxplot> print nu
340.9781 THz
This maximum could also be sought be searching for turning points in the function
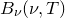 , i.e. by solving the equation
, i.e. by solving the equation ![\[ \frac{\mathrm{d}B_\nu (\nu ,T)}{\mathrm{d}\nu }=0. \]](images/img-0151.png) |
pyxplot> nu = 2e14*unit(Hz)
pyxplot> solve diff_dv(phy.Bv(v,5800*unit(K)),nu) =

.......> unit(0*W/Hz**2/m**2/sterad) via nu
pyxplot> print nu
340.9781 THz
Finally, this maximum could also be found using Pyxplot’s built-in function Bvmax(T):
pyxplot> print phy.Bvmax(5800*unit(K))
340.97806 THz