C.1 Notation

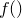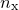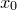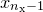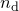I shall assume that we have some function $f()$ , which takes $n_\mathrm {x}$ parameters, $x_0$ ... $x_{n_\mathrm {x}-1}$ , the set of which may collectively be written as the vector $\mathbf{x}$ . We are supplied a datafile, containing a number $n_\mathrm {d}$ of datapoints, each consisting of a set of values for each of the 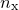$n_\mathrm {x}$ parameters, and one for the value which we are seeking to make 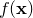$f(\mathbf{x})$ match. I shall call of parameter values for the 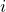$i$ th datapoint 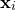$\mathbf{x}_ i$ , and the corresponding value which we are trying to match 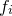$f_ i$ . The data file may contain error estimates for the values 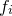$f_ i$ , which I shall denote 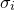$\sigma _ i$ . 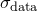If these are not supplied, then I shall consider these quantities to be unknown, and equal to some constant $\sigma _\mathrm {data}$ .

Finally, I assume that there are 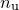$n_\mathrm {u}$ coefficients within the function 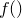$f()$ that we are able to vary, corresponding to those variable names listed after the via statement in the fit command. I shall call these coefficients 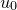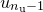$u_0$ ... $u_{n_\mathrm {u}-1}$ , and refer to them collectively as $\mathbf{u}$ .

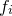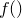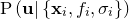I model the values $f_ i$ in the supplied data file as being noisy Gaussian-distributed observations of the true function $f()$ , and within this framework, seek to find that vector of values $\mathbf{u}$ which is most probable, given these observations. The probability of any given $\mathbf{u}$ is written $\mathrm{P}\left( \mathbf{u} | \left\{ \mathbf{x}_ i, f_ i, \sigma _ i \right\} \right)$ .