Pyxplot Users' Guide: Color scale bars

8.12.2 Color scale bars

By default, plots with color maps with single-parameter color mappings are accompanied by color scale bars, which appear by default on the right-hand side of the plot. Such scale bars may be configured using the set colorkey command. Issuing the command

set colorkey

by itself causes such a scale to be drawn on graphs in the default position, usually along the right-hand edge of the graphs. The converse action is achieved by:

set nocolorkey

The command

unset colorkey

causes Pyxplot to revert to its default behaviour, as specified in a configuration file, if present. A position for the key may optionally be specified after the set colorkey command, as in the example:

set colorkey bottom

Recognised positions are top, bottom, left and right. above is an alias for top; below is an alias for bottom and outside is an alias for right.

The format of the ticks along such scale bars may be set using the set c1format command command, which is similar in syntax to the set xformat command (see Section 8.8.8), but which uses c as its dummy variable.

The positions of the ticks along color scale bars may be set using the set c1tics command command, which has similar syntax to the set xtics command.

Example: An image of the Mandelbrot set

The Mandelbrot set is a set of points in the complex plane whose boundary forms a fractal with a Hausdorff dimension of two. A point $c$ in the complex plane is defined to lie within the Mandelbrot set if the complex sequence of numbers

$z_{n+1} = z_ n^2 + c,$

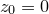subject to the starting condition $z_0=0$ , remains bounded.
The map of this set of points has become a widely-used image of the power of chaos theory to produce complicated structure out of simple algorithms. To produce a more pleasing image, points in the complex plane are often colored differently, depending on how many iterations 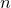$n$ of the above series are required for 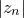$|z_ n|$ to exceed 2. This is the point of no return, beyond which it can be shown that 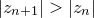$|z_{n+1}|>|z_ n|$ and that divergence is guaranteed. 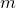In numerical implementations of the above iteration, in the absence of any better way to prove that the iteration remains bounded for a certain value of $c$ , some maximum number of iterations $m$ is chosen, and the series is deemed to have remained bounded if 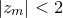$|z_ m|<2$ . 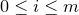This is implemented in Pyxplot by the built-in mathematical function fractal_mandelbrot(z,m), which returns an integer in the range $0\leq i\leq m$ .
set numerics complex
set sample grid 500x500
set size square
set nokey
set nocolkey
set log c1
plot [-2:2][-2:2] fractals.mandelbrot(x+i*y,70)+1 with colormap
$\includegraphics[width=8cm]{examples/eps/ex_mandelbrot}$