8.12 Color maps

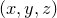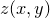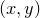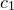Color maps provide a graphical means of producing two-dimensional representations of $(x,y,z)$ surfaces, or equivalently of producing maps of the values $z(x,y)$ of functions of two variables. Each point in the $(x,y)$ plane is assigned a color which indicates the value $z$ associated with that point. In this section, we refer to the third coordinate as $c_1$ rather than $z$ , to distinguish it from the third axes of three-dimensional plots¹.

In the following simple example, a color map of the complex argument of the Riemann zeta function 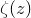$\zeta (z)$ is produced, taking the 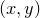$(x,y)$ plane to be an Argand plane, with 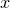$x$ being the real axis, and 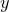$y$ being the imaginary axis. Each point in the plane has an associated value of $c_1$ .

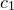set numerics complex
set nokey
set size 8 square
set samples grid 400x400
set c1range[-pi:pi]
set c1format r"$%spi$"%(c/pi)
plot [-20:6][-13:13] arg(zeta(x+i*y)) with colormap

$\includegraphics[width=8cm]{examples/eps/ex_zeta_arg}$

The set c1range command sets the range of values of 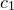$c_1$ to be assigned colors between black and white. By default, the lowest and highest values of 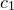$c_1$ found in the color map is assigned to black and white.

The set c1format command controls the format of the axis labels placed along the color scale bar on the right-hand side of the plot. In this case, they are marked as multiples of 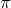$\pi$ .

The set samples grid command sets the dimensions of the grid of samples – or pixels – used to render the color map. If either value is replaced with an asterisk (*) then the current number of samples set in the set samples command is substituted.

If a data file is supplied to the colormap plot style, then the datapoints need not lie on the specified regular grid, but are first re-sampled onto this grid using the interpolation method specified using the set samples interpolate command (see Section 5.7). Three methods are available. nearestNeighbor uses the value of 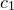$c_1$ associated with the datapoint closest to each grid point, producing color maps which look like Voronoi diagrams. inverseSquare interpolation returns a weighted average of the supplied data points, using the inverse squares of their distances from each grid point as weights. monaghanLattanzio interpolation uses the weighting function of Monaghan & Lattanzio (1985) which is described further in Section 5.7).

In the following example, a color map of a quadrupole is produced using four input datapoints:

set nokey
set size 8 square
set samples grid 200x200 interpolate inverseSquare
plot [-4:4][-4:4] ’–’ with colormap
-1 -1  1
-1  1 -1
1 -1 -1
1  1  1
END

$\includegraphics[width=8cm]{examples/eps/ex_quadrupole}$

Footnotes

When color maps are plotted on three-dimensional graphs, they appear in a flat plane on one of the back faces of the plot selected using the axes modifier to the plot command, and the 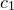$c_1$ -axis associated with each are entirely independent of the plot’s $z$ -axis.