Previous: The exceptions module Up: List of in-built functions Next: The os module  
: Reference manual : List of in-built functions : The fractals module

12.4 The fractals module

fractals.julia($z$,$z_ c$,$m$)
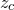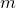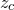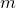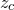The fractals.julia($z$,$z_ c$,$m$) function tests whether the point $z$ in the complex plane lies within the Julia set associated with the point $z_ c$ in the complex plane. The expression 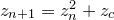$z_{n+1} = z_ n^2 + z_ c$ is iterated until either 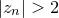$|z_ n|>2$, in which case the iteration is deemed to have diverged, or until 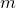$m$ iterations have been exceeded, in which case it is deemed to have remained bounded. The number of iterations required for divergence is returned, or 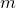$m$ is returned if the iteration remained bounded – i.e. the point lies within the numerical approximation to the Julia set.

fractals.mandelbrot($z$,$m$)
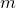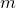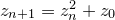The fractals.mandelbrot($z$,$m$) function tests whether the point $z$ in the complex plane lies within the Mandelbrot set. The expression $z_{n+1} = z_ n^2 + z_0$ is iterated until either 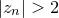$|z_ n|>2$, in which case the iteration is deemed to have diverged, or until 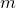$m$ iterations have been exceeded, in which case it is deemed to have remained bounded. The number of iterations required for divergence is returned, or 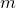$m$ is returned if the iteration remained bounded – i.e. the point lies within the numerical approximation to the Mandelbrot set.

Previous: The exceptions module Up: List of in-built functions Next: The os module