5.7 Datafile interpolation

The interpolate command can be used to generate a special function within Pyxplot’s mathematical environment which interpolates a set of data points supplied from a data file. As with other commands, data can also be supplied from functions, or from a colon-separated list of vectors (see Section 6.5.3). Either one- or two-dimensional interpolation is possible. Two-dimensional interpolation is described in the next section.

In the case of one-dimensional interpolation, various different types of interpolation are supported: linear interpolation, power law interpolation, polynomial interpolation, cubic spline interpolation and akima spline interpolation. Stepwise interpolation returns the value of the datapoint nearest to the requested point in argument space. The use of polynomial interpolation with large datasets is strongly discouraged, as polynomial fits tend to show severe oscillations between data points.

Except in the case of stepwise interpolation, extrapolation is not permitted; if an attempt is made to evaluate an interpolated function beyond the limits of the data points which it interpolates, Pyxplot returns an error or value of not-a-number. This behaviour can be configured using the set numeric errors quiet command (see Section 4.4).

The interpolate command has similar syntax to the fit command:

interpolate ( akima | linear | loglinear | polynomial |
              spline | stepwise |
              2d [( bmp_r | bmp_g | bmp_b )] )
            [<range specification>] <function name>"()"
            '<filename>'
            [ every <expression> {:<expression} ]
            [ index <value> ]
            [ select <expression> ]
            [ using <expression> {:<expression} ]

A very common application of the interpolate command is to perform arithmetic functions such as addition or subtraction on datasets which are not sampled at the same abscissa values. The following example would plot the difference between two such datasets:

interpolate linear f() 'data1.dat'
interpolate linear g() 'data2.dat'
plot [min:max] f(x)-g(x)

Note that it is advisable to supply a range to the plot command in this example: because the two datasets have been turned into continuous functions, the plot command has to guess a range over which to plot them, unless one is explicitly supplied.

The spline command is an alias for interpolate spline; the following two statements are equivalent:

spline f() 'data1.dat'
interpolate spline f() 'data1.dat'

Example: A demonstration of the linear, spline and akima modes of interpolation

In this example, we demonstrate the linear, spline and akima modes of interpolation using an example data file with non-smooth data generated using the tabulate command (see Section 5.5):
f(x) = 0
f(x)[0:1] = 0.5
f(x)[2:4] = cos((x-3)*pi/2)
set samples 20
tabulate [0:4] f(x)
Having set three functions to interpolate these non-smooth data in different ways, we plot them with a vertical offset of 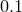$0.1$ between them for clarity. The interpolated data fileis plotted with points three times to show where each of the interpolation functions is pinned.
interpolate linear f_linear() "interpolation.dat"
interpolate spline f_spline() "interpolation.dat"
interpolate akima  f_akima () "interpolation.dat"

set key top left
plot [0:4][-0.1:1.3]
   "interpolation.dat" using 1:($2+0.0) notitle with points pt 1,
   f_linear(x)+0.0 title "Linear",
   "interpolation.dat" using 1:($2+0.1) notitle with points pt 1,
   f_spline(x)+0.1 title "Spline",
   "interpolation.dat" using 1:($2+0.2) notitle with points pt 1,
   f_akima (x)+0.2 title "Akima"
The resulting plot is shown below:
$\includegraphics[width=\textwidth ]{examples/eps/ex_interpolation}$