C.2 The probability density function

Bayes’ Theorem states that:

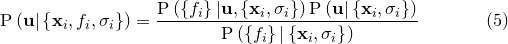$\begin{equation} \mathrm{P}\left( \mathbf{u} | \left\{ \mathbf{x}_ i, f_ i, \sigma _ i \right\} \right) = \frac{ \mathrm{P}\left( \left\{ f_ i \right\} | \mathbf{u}, \left\{ \mathbf{x}_ i, \sigma _ i \right\} \right) \mathrm{P}\left( \mathbf{u} | \left\{ \mathbf{x}_ i, \sigma _ i \right\} \right) }{ \mathrm{P}\left( \left\{ f_ i \right\} | \left\{ \mathbf{x}_ i, \sigma _ i \right\} \right) } \end{equation}$

(C.1)

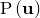Since we are only seeking to maximise the quantity on the left, and the denominator, termed the Bayesian evidence, is independent of $\mathbf{u}$ , we can neglect it and replace the equality sign with a proportionality sign. Furthermore, if we assume a uniform prior, that is, we assume that we have no prior knowledge to bias us towards certain more favoured values of $\mathbf{u}$ , then $\mathrm{P}\left( \mathbf{u} \right)$ is also a constant which can be neglected. 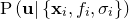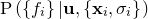We conclude that maximising $\mathrm{P}\left( \mathbf{u} | \left\{ \mathbf{x}_ i, f_ i, \sigma _ i \right\} \right)$ is equivalent to maximising $\mathrm{P}\left( \left\{ f_ i \right\} | \mathbf{u}, \left\{ \mathbf{x}_ i, \sigma _ i \right\} \right)$ .

Since we are assuming 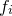$f_ i$ to be Gaussian-distributed observations of the true function 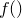$f()$ , this latter probability can be written as a product of 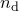$n_\mathrm {d}$ Gaussian distributions:

$\begin{equation} \mathrm{P}\left( \left\{ f_ i \right\} | \mathbf{u}, \left\{ \mathbf{x}_ i, \sigma _ i \right\} \right) = \prod _{i=0}^{n_\mathrm {d}-1} \frac{1}{\sigma _ i\sqrt {2\pi }} \exp \left( \frac{ -\left[f_ i - f_\mathbf {u}(\mathbf{x}_ i)\right]^2 }{ 2 \sigma _ i^2 } \right) \end{equation}$

(C.2)

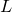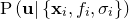The product in this equation can be converted into a more computationally workable sum by taking the logarithm of both sides. Since logarithms are monotonically increasing functions, maximising a probability is equivalent to maximising its logarithm. We may write the logarithm $L$ of $\mathrm{P}\left( \mathbf{u} | \left\{ \mathbf{x}_ i, f_ i, \sigma _ i \right\} \right)$ as:

$\begin{equation} L = \sum _{i=0}^{n_\mathrm {d}-1} \left( \frac{ -\left[f_ i - f_\mathbf {u}(\mathbf{x}_ i)\right]^2 }{ 2 \sigma _ i^2 } \right) + k \end{equation}$

(C.3)

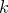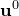where $k$ is some constant which does not affect the maximisation process. It is this quantity, the familiar sum-of-square-residuals, that we numerically maximise to find our best-fitting set of parameters, which I shall refer to from here on as $\mathbf{u}^0$ .