C.5 The correlation matrix

Having evaluated the covariance matrix, we may straightforwardly find the standard deviations in each of our variables, by taking the square roots of the terms along its leading diagonal. For datafiles where the user does not specify the standard deviations 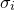$\sigma _ i$ in each value 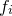$f_ i$ , the task is not quite complete, as the Hessian matrix depends critically upon these uncertainties, even if they are assumed the same for all of our 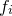$f_ i$ . This point is returned to in Section C.6.

The correlation matrix $\mathbf{C}$ , whose terms are given by:

$\begin{equation} C_{ij} = \frac{V_{ij}}{\sigma _ i\sigma _ j} \end{equation}$

(C.16)

may be considered a more user-friendly version of the covariance matrix for inspecting the correlation between parameters. The leading diagonal terms are all clearly equal unity by construction. The cross terms lie in the range 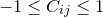$-1 \leq C_{ij} \leq 1$ , the upper limit of this range representing perfect correlation between parameters, and the lower limit perfect anti-correlation.