C.4 The covariance matrix
The terms of the covariance matrix 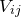 are defined by:
are defined by:
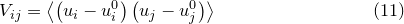 |
(C.8) |
Its leading diagonal terms may be recognised as equalling the variances of each of our 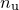 variables; its cross terms measure the correlation between the variables. If a component
variables; its cross terms measure the correlation between the variables. If a component 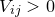 , it implies that higher estimates of the coefficient
, it implies that higher estimates of the coefficient 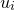 make higher estimates of
make higher estimates of 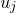 more favourable also; if
more favourable also; if 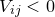 , the converse is true.
, the converse is true.
It is a standard statistical result that 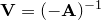 . In the remainder of this section we prove this; readers who are willing to accept this may skip onto Section C.5.
. In the remainder of this section we prove this; readers who are willing to accept this may skip onto Section C.5.
Using 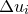 to denote
to denote 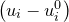 , we may proceed by rewriting Equation () as:
, we may proceed by rewriting Equation () as:
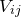 |
 |
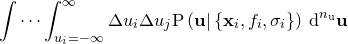 |
(C.9) | ||
 |
 |
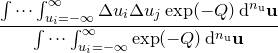 |
The normalisation factor in the denominator of this expression, which we denote as 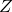 , the partition function, may be evaluated by
, the partition function, may be evaluated by 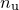 -dimensional Gaussian integration, and is a standard result:
-dimensional Gaussian integration, and is a standard result:
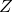 |
 |
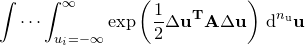 |
(C.10) | ||
 |
 |
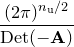 |
Differentiating 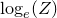 with respect of any given component of the Hessian matrix
with respect of any given component of the Hessian matrix 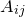 yields:
yields:
![\begin{equation} -2 \frac{\partial }{\partial A_{ij}} \left[ \log _ e(Z) \right] = \frac{1}{Z} \idotsint _{u_ i=-\infty }^{\infty } \Delta u_ i \Delta u_ j \exp (-Q) \, \mathrm{d}^{n_\mathrm {u}}\mathbf{u} \end{equation}](images/img-0890.png) |
(C.11) |
which we may identify as equalling 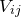 :
:
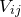 |
 |
![$\displaystyle -2 \frac{\partial }{\partial A_{ij}} \left[ \log _ e(Z) \right] $](images/img-0892.png) |
(C.12) | ||
 |
 |
![$\displaystyle -2 \frac{\partial }{\partial A_{ij}} \left[ \log _ e((2\pi )^{n_\mathrm {u}/2}) - \log _ e(\mathrm{Det}(\mathbf{-A})) \right] \nonumber $](images/img-0893.png) |
|||
 |
 |
![$\displaystyle 2 \frac{\partial }{\partial A_{ij}} \left[ \log _ e(\mathrm{Det}(\mathbf{-A})) \right] \nonumber $](images/img-0894.png) |
This expression may be simplified by recalling that the determinant of a matrix is equal to the scalar product of any of its rows with its cofactors, yielding the result:
![\begin{equation} \frac{\partial }{\partial A_{ij}} \left[\mathrm{Det}(\mathbf{-A})\right] = -a_{ij} \end{equation}](images/img-0895.png) |
(C.13) |
where 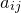 is the cofactor of
is the cofactor of 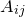 . Substituting this into Equation () yields:
. Substituting this into Equation () yields:
 |
(C.14) |
Recalling that the adjoint 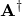 of the Hessian matrix is the matrix of cofactors of its transpose, and that
of the Hessian matrix is the matrix of cofactors of its transpose, and that 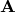 is symmetric, we may write:
is symmetric, we may write:
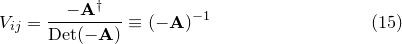 |
(C.15) |
which proves the result stated earlier.