12.9 The stats module
The stats module contains statistical functions:
stats.binomialCDF(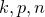 )
)
The stats.binomialCDF(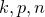 ) function evaluates the probability of getting fewer than or exactly
) function evaluates the probability of getting fewer than or exactly 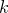 successes out of
successes out of 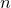 trials in a binomial distribution with success probability
trials in a binomial distribution with success probability 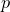 .
. 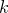 and
and 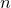 must be positive real integers.
must be positive real integers. 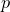 must be a real number in the range
must be a real number in the range 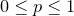 .
.
stats.binomialPDF(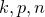 )
)
The stats.binomialPDF(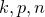 ) function evaluates the probability of getting
) function evaluates the probability of getting 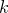 successes out of
successes out of 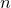 trials in a binomial distribution with success probability
trials in a binomial distribution with success probability 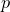 .
. 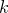 and
and 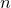 must be positive real integers.
must be positive real integers. 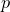 must be a real number in the range
must be a real number in the range 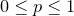 .
.
stats.chisqCDF(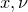 )
)
The stats.chisqCDF(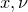 ) function returns the cumulative probability density at
) function returns the cumulative probability density at  in a
in a 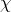 -squared distribution with
-squared distribution with  degrees of freedom.
degrees of freedom.  must be a positive real dimensionless integer.
must be a positive real dimensionless integer.  must be a positive real dimensionless number.
must be a positive real dimensionless number.
stats.chisqCDFi(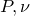 )
)
The stats.chisqCDFi(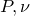 ) function returns the point
) function returns the point  at which the cumulative probability density in a
at which the cumulative probability density in a 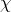 -squared distribution with
-squared distribution with  degrees of freedom is
degrees of freedom is 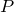 .
.  must be a positive real dimensionless integer.
must be a positive real dimensionless integer. 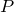 must be a real number in the range
must be a real number in the range 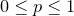 .
.
stats.chisqPDF(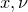 )
)
The stats.chisqPDF(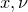 ) function returns the probability density at
) function returns the probability density at  in a
in a 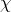 -squared distribution with
-squared distribution with  degrees of freedom.
degrees of freedom.  must be a positive real dimensionless integer.
must be a positive real dimensionless integer.  must be a positive real dimensionless number.
must be a positive real dimensionless number.
stats.gaussianCDF(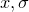 )
)
The stats.gaussianCDF(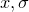 ) function evaluates the Gaussian cumulative distribution function of standard deviation
) function evaluates the Gaussian cumulative distribution function of standard deviation 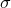 at
at  . The distribution is centred upon
. The distribution is centred upon 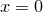 .
.  and
and 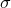 must both be real, but may have any physical dimensions so long as they match.
must both be real, but may have any physical dimensions so long as they match.
stats.gaussianCDFi(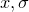 )
)
The stats.gaussianCDFi(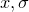 ) function evaluates the inverse Gaussian cumulative distribution function of standard deviation
) function evaluates the inverse Gaussian cumulative distribution function of standard deviation 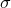 at
at  . The distribution is centred upon
. The distribution is centred upon 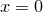 .
.  and
and 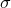 must both be real, but may have any physical dimensions so long as they match.
must both be real, but may have any physical dimensions so long as they match.
stats.gaussianPDF(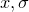 )
)
The stats.gaussianPDF(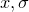 ) function evaluates the Gaussian probability density function of standard deviation
) function evaluates the Gaussian probability density function of standard deviation 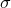 at
at  . The distribution is centred upon
. The distribution is centred upon 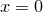 .
.  and
and 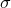 must both be real, but may have any physical dimensions so long as they match.
must both be real, but may have any physical dimensions so long as they match.
stats.lognormalCDF(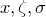 )
)
The stats.lognormalCDF(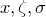 ) function evaluates the log normal cumulative distribution function of standard deviation
) function evaluates the log normal cumulative distribution function of standard deviation 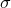 , centred upon
, centred upon 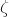 , at
, at  .
. 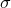 must be real, positive and dimensionless.
must be real, positive and dimensionless.  and
and 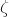 must both be real, but may have any physical dimensions so long as they match.
must both be real, but may have any physical dimensions so long as they match.
stats.lognormalCDFi(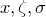 )
)
The stats.lognormalCDFi(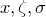 ) function evaluates the inverse log normal cumulative distribution function of standard deviation
) function evaluates the inverse log normal cumulative distribution function of standard deviation 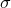 , centred upon
, centred upon 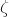 , at
, at  .
. 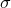 must be real, positive and dimensionless.
must be real, positive and dimensionless.  and
and 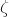 must both be real, but may have any physical dimensions so long as they match.
must both be real, but may have any physical dimensions so long as they match.
stats.lognormalPDF(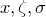 )
)
The stats.lognormalPDF(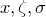 ) function evaluates the log normal probability density function of standard deviation
) function evaluates the log normal probability density function of standard deviation 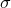 , centred upon
, centred upon 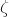 , at
, at  .
. 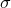 must be real, positive and dimensionless.
must be real, positive and dimensionless.  and
and 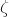 must both be real, but may have any physical dimensions so long as they match.
must both be real, but may have any physical dimensions so long as they match.
stats.poissonCDF(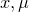 )
)
The stats.poissonCDF(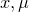 ) function returns the probability of getting
) function returns the probability of getting 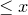 from a Poisson distribution with mean
from a Poisson distribution with mean 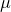 , where
, where 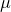 must be real, positive and dimensionless and
must be real, positive and dimensionless and  must be real and dimensionless.
must be real and dimensionless.
stats.poissonPDF(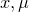 )
)
The stats.poissonPDF(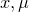 ) function returns the probability of getting
) function returns the probability of getting  from a Poisson distribution with mean
from a Poisson distribution with mean 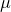 , where
, where 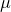 must be real, positive and dimensionless and
must be real, positive and dimensionless and  must be a real dimensionless integer.
must be a real dimensionless integer.
stats.tdistCDF(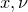 )
)
The stats.tdistCDF(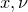 ) function returns the cumulative probability density at
) function returns the cumulative probability density at  in a
in a 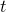 -distribution with
-distribution with  degrees of freedom.
degrees of freedom.  must be a positive real dimensionless integer.
must be a positive real dimensionless integer.  must be a positive real dimensionless number.
must be a positive real dimensionless number.
stats.tdistCDFi(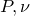 )
)
The stats.tdistCDFi(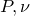 ) function returns the point
) function returns the point  at which the cumulative probability density in a
at which the cumulative probability density in a 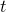 -distribution with
-distribution with  degrees of freedom is
degrees of freedom is 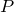 .
.  must be a positive real dimensionless integer.
must be a positive real dimensionless integer. 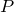 must be a real number in the range
must be a real number in the range 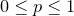 .
.
stats.tdistPDF(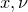 )
)
The stats.tdistPDF(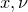 ) function returns the probability density at
) function returns the probability density at  in a
in a 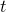 -distribution with
-distribution with  degrees of freedom.
degrees of freedom.  must be a positive real dimensionless integer.
must be a positive real dimensionless integer.  must be a positive real dimensionless number.
must be a positive real dimensionless number.