Pyxplot Users' Guide: The random module

12.8 The `random` module

The random module contains function for generating random samples from probability distributions:

random.binomial(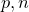 $p,n$ )
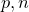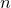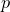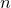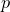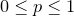The random.binomial( $p,n$ ) function returns a random sample from a binomial distribution with $n$ independent trials and a success probability $p$ . $n$ must be a real positive dimensionless integer. $p$ must be a dimensionless number in the range $0\leq p\leq 1$ .

random.chisq( $\nu$ )
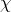The random.chisq( $\nu$ ) function returns a random sample from a $\chi$ -squared distribution with $\nu$ degrees of freedom, where $\nu$ must be a real positive dimensionless integer.

random.gaussian(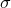 $\sigma$ )
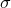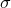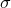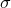The random.gaussian( $\sigma$ ) function returns a random sample from a Gaussian (normal) distribution of standard deviation $\sigma$ and centred upon zero. $\sigma$ must be real, but may have any physical units. The returned random sample shares the physical units of $\sigma$ .

random.lognormal(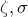 $\zeta ,\sigma$ )
The random.lognormal(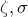 $\zeta ,\sigma$ ) function returns a random sample from the log normal distribution centred on 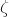$\zeta$ , and of width 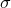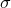$\sigma$ . $\sigma$ must be a real positive dimensionless number. 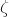$\zeta$ must be real, but may have any physical units. The returned random sample shares the physical units of $\zeta$ .

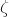random.poisson(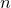 $n$ )
The random.poisson(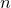 $n$ ) function returns a random integer from a Poisson distribution with mean 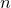$n$ , where 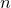$n$ must be a real positive dimensionless number.

random.random()
The random.random() function returns a random real number between 0 and 1.

random.tdist( $\nu$ )
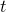The random.tdist( $\nu$ ) function returns a random sample from a $t$ -distribution with $\nu$ degrees of freedom, where $\nu$ must be a real positive dimensionless integer.

12.8 The random module

12.8 The `random` module